안녕하세요, 기버보이입니다.
오늘은 '피타고라스의 정리'에 대해서 공부하겠습니다.
고대 그리스의 유명한 수학자 피타고라스가 발견한 정리라고 해서 붙여진 이름 인데요.
'피타고라스가 발견했다 안했다.' 해서 말이 많은 정리 입니다.
피타고라스의 정리는 '직각삼각형에서 빗변의 길의 제곱은
나머지 양 변의 제곱의 합과 같다.'라는 것을 의미해요.
전기기사에서는 임피던스의 크기, 전하의 거리, 역률 등을 계산할 때, 주로 사용됩니다. 여러가지로 응용도 합니다.
피타고라스의 정리가 성립되기 위해 꼭 필요한 조건은 직각삼각형이어야만 합니다.
어렵지 않으니 차근차근 하나씩 이해해 나가기로 해요.
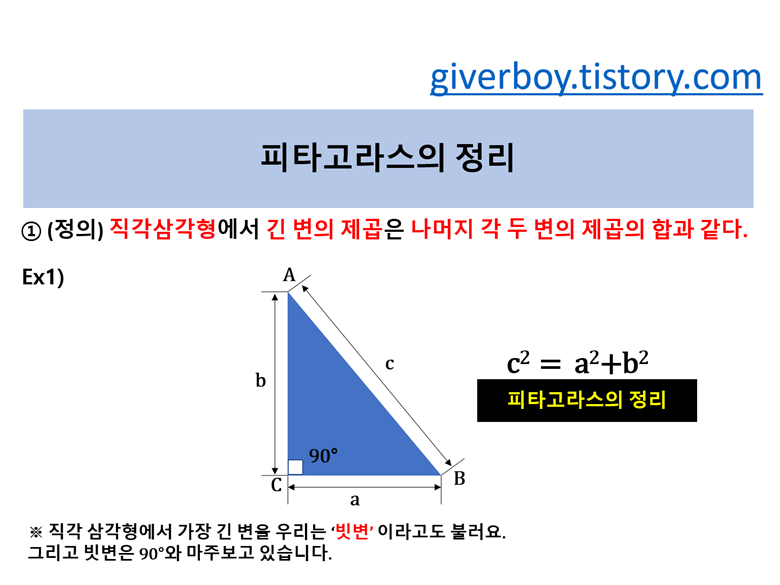
① 피타고라스의 정리에 대해서 간단히 적어보았어요.
각도 90도와 마주보고 있는 가장 긴 변은 나머지 두변의 각 제곱의 합과 같아요. 이해하셨나요?
여기서 조심해야 되는 조건은 반드시 직각삼각형에서만 성립한다는 부분 입니다. 잊지마세요.
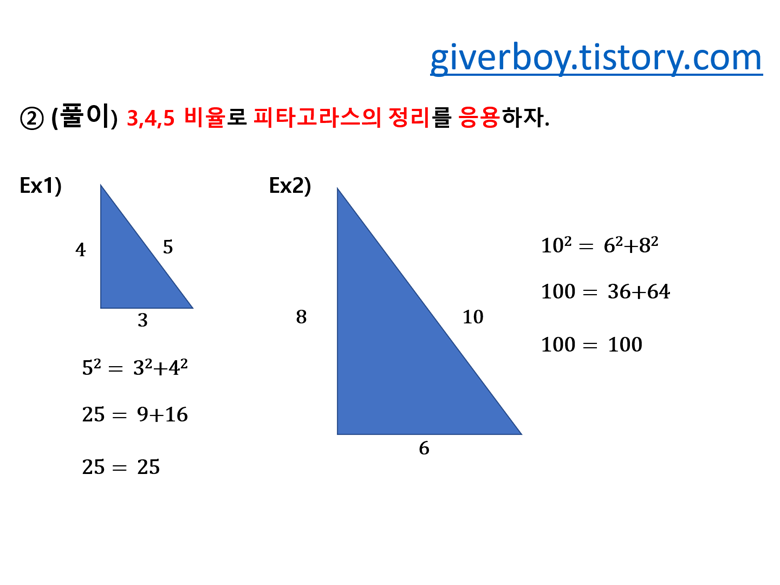
② 3.4.5의 비율은 직각삼각형의 가장 기본이 되는 비율이죠.
가장 긴 변을 5라고 하면 나머지 두 변은 3과 4의 비율을 가져요.
가급적 전기기초수학에서는 기초를 다지기 위해서 전기기사 이론 이야기를 배제하려고 하는데요.
이번에 하나만 이야기 할께요.
저항이 3Ω이고 리액턴스가 4Ω이면, 임피던스는 5Ω이예요. 굳이 피타고라스의 정리를 몰라도 되지요.
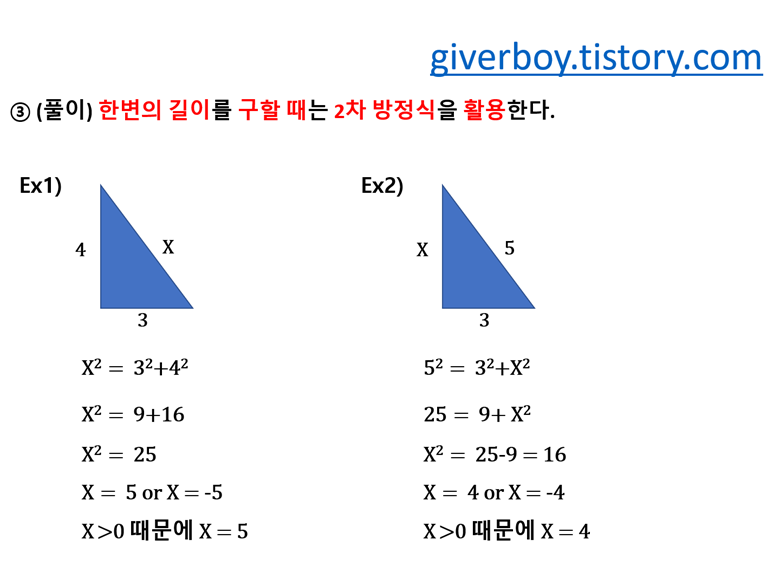
③ 2차 방정식의 답을 구하는 방법을 배웠죠?
직각삼각형에서 구해야 하는 변을 미지수 X라고 하면, 피타고라스의 정리에 의해서 식을 만들 수 있어요.
그리고 2차 방정식의 답을 구하면 됩니다.
피타고라스의 정리는 전기기사나 전기공사기사 등 에서 사용이 됩니다.
어려운 부분은 아니니, 꼭 외우시길 바래요.
기초가 단단해야 나중에 문제를 쉽게 풀 수 있어요.
항상 여러분의 꿈을 응원합니다.
감사합니다.
'전기기초수학' 카테고리의 다른 글
| [전기수학기초-21강]함수의 기초 및 1차 함수 (1) | 2020.12.03 |
|---|---|
| [전기수학기초-20강]좌표의 이해 (1) | 2020.11.22 |
| [전기수학기초-18강]방정식의 이해 (2) | 2020.11.10 |
| [전기수학기초-17강]인수분해의 이해 (1) | 2020.11.02 |
| [전기수학기초-16강]다항식의 이해 (1) | 2020.10.28 |