안녕하세요, 기버보이입니다.
오늘은 함수에 대해서 알아보겠습니다.
우리는 등식이 아닌 다항식을 정리하는 방법을 배웠고, 방정식의 해를 구하는 방법들도 배웠어요.
함수는 그것보다는 한 단계 위의 공부예요.
다항식은 식을 정리하는 과정이었고, 방정식은 단항식이나
다항식에서 답을 구하는 과정이었죠.
함수는 두 변수 x,y에 대하여 일정한 관계가 있을 때, 두 식의 관계를 구하는 과정이예요. 말이 좀 어렵죠.
이해만 하면 전혀 어렵지 않아요.
전기공학에서는 외우는 공식들이 다 이 함수 과정이예요.
(이해하고 공부하면 많이 도움이 되요.)
x를 입력, y를 출력이라고 가정하면 이해가 쉬워요.
tv리모콘의 볼륨버튼을 생각하면 되는데요.
리모콘 볼륨 1씩 올리면, 스피커소리도 그에 맞게 커지잖아요.
그래서 우리는 볼륨 10 이 볼륨 1보다 소리가 훨~~씬 크다는 것을 알고 있죠.
결국, 볼륨입력과 스피커 출력 사이에는 일정한 관계가 있다는 것을 추측할 수 있죠. 여기에서 이 일정한 관계를 함수라고 생각하시면 됩니다.

함수란, 두 변수 x,y의 관계를 나타낸 식이예요.
그림처럼 입력이 0, 1, 2, 3, 4 출력이 0, 2, 4, 6 ,8이면
입력과 출력은 y=2x 라는 시스템을 만들 수 있는 거죠.
만약, 이 함수 시스템에 입력 -1 을 넣으면 출력 -2를 예상할 수가 있어요. 입력이 10 이면 출력 20을 예상할 수 있는 거예요.
결국 함수란, x와 y의 관계를 정의한 식이라고 이해하세요.
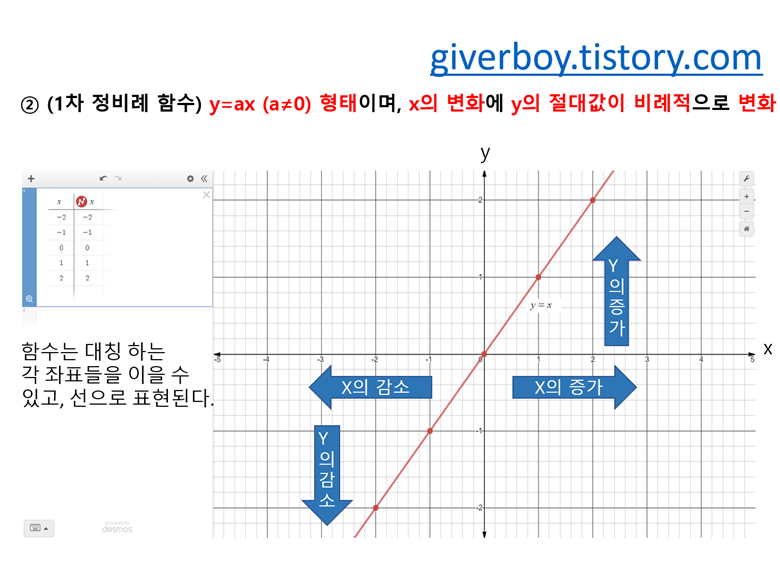
정비례 함수란, y=ax꼴의 함수를 말해요.
a=0이면 정비례함수가 성립이 안됩니다.
그림처럼 a가 0보다 크면, 원점을 지나는 y=ax그래프는 1사분면과 3사분면을 지나고요.
a가 0보다 작으면, 원점을 지나는 y=ax그래프는 2사분면과 4사분면을 지납니다.
(그림에는 표현 못했네요. 추후에 업데이트 할께요.)

y=ax형태의 함수에서 a의 절대값이 크면 그 기울기는 그림처럼 경사가 커지게 됩니다. 그리고 a가 양수이냐 음수이냐에 따라서 그래프 선의 위치는 달라지게 되고,
a의 값이 부호는 서로 y축 대칭이게 됩니다.
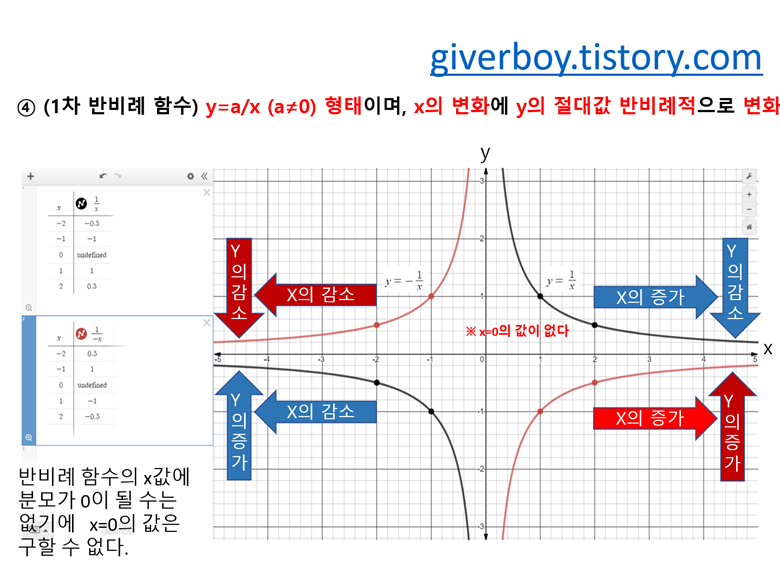
반비례 함수에서 중요한 점은 'a= 0이 되면 반비례함수가 성립이 안된다.'는 점과 'x값에 0을 넣을 수 없다.'는 거예요.
극한을 공부하게 되면 반비례 함수에 대해서 다시 만날 수 있을 거예요.
여기에서는 그래프의 모양만 익히세요.

대칭이동은 y=x그래프를 기준으로 설명해보았어요.
만약 y=x그래프를 x축 방향으로 1만큼 이동하면(오른쪽으로 1만큼 이동), y=x-1이 됩니다.
그리고 y=x의 그래프를 x축 방향으로 -1만큼 이동하면(왼쪽으로 1만큼 이동), y=x+1이 됩니다.
여기에서 중요한 점은 이동하고 싶은 위치가 식에서는 반대 부호라는 점이죠. 잊지마세요.
그래프를 PPT로 그리려 하니, 완전 노가다라더구요.
그래서 무료그래프 그리는 방법을 찾다가 구글에서 demos.com이라는 사이트에서 그래프를 쉽게 그리는 수학용 툴을 이용했어요.
다양한 수학용 툴이 있으니, 좀 더 세부적으로 공부하고 싶은 분은 이용하셔도 좋을 듯 해요.
저도 그래프를 그려야 하면 이 곳 도움을 받으려고 합니다.
항상 여러분의 꿈을 응원 합니다. 힘내세요.
부족한 글 읽어주셔서 감사드립니다.
'전기기초수학' 카테고리의 다른 글
| [전기수학기초-23강]삼각비의 이해 (0) | 2020.12.29 |
|---|---|
| [전기수학기초-22강]2차 함수 및 3차 함수 (1) | 2020.12.15 |
| [전기수학기초-20강]좌표의 이해 (1) | 2020.11.22 |
| [전기수학기초-19강]피타고라스의 정리 (3) | 2020.11.10 |
| [전기수학기초-18강]방정식의 이해 (2) | 2020.11.10 |