안녕하세요, 기버보이입니다.
오늘은 '2차 함수와 3차 함수'에 대해서 알아보겠습니다.
앞서 공부한 1차 함수는 어떠셨나요?
전기기사에서 적어도 3차함수까지는 알아된다고 개인적으로 생각해요.
2차 함수는 y=f(x)의 함수에서 x의 차수가 2차인 함수이고,
3차 함수는 y=f(x)의 함수에서 x의 차수가 3차인 함수입니다.
2차 함수와 3차 함수 그래프는 전기기사에서 종종 다루죠.
깊게 알 필요는 없지만, 적어도 모양은 익히고 가도록 해요.
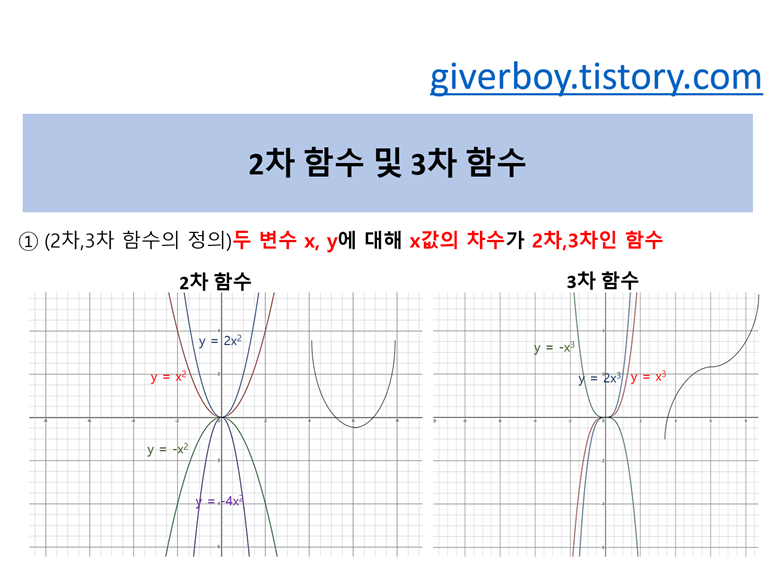
① 2차 함수와 3차 함수는 y=f(x)라는 함수에서 x의 차수가 2차인 함수, 3차인 함수를 각각 이야기 합니다.
대칭이동이 없다면, 2차 함수의 기본형인 y=ax^2은 알파벳 'U'와 같은 모양 입니다.
이 함수는 원점을 지나게 되고, y축을 중심으로 데칼코마니와 같이 접히는 모양을 가지게 됩니다.
역시 대칭 이동이 없다면, 3차 함수의 기본형인 y=ax^3은 '~'와 같은 모양입니다.
이 함수는 원점을 지나게 되고, 원점을 중심으로 접히는 모양을 가지게 됩니다.
여기에서 원점을 중심으로 접히는 모양이란, x축으로 한번 y축으로 한번 대칭 시킨다는 의미입니다.
결국, 원점을 중심으로 접히는 모양을 가지게 되는 거죠.
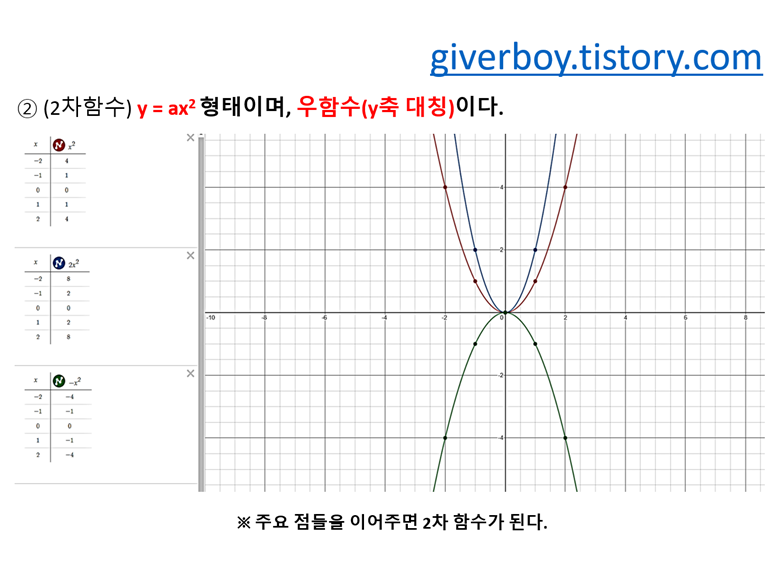
② 2차 함수의 각 좌표를 이으면, 결국 함수는 선으로 표현되게 됩니다.
모양은 앞서 말한 바와 같이 U와 같은 모양을 가지게 되죠.
여기에서 우함수라는 개념이 나오는데요.
우함수란, 어떠한 함수가 y축 대칭인 함수를 말해요.
f(-x)=f(x)라고 표현하는데, 이 말은 입력 x값과 입력 -x값이 같은 출력 y를 가진다는 것을 알 수 있어요.
y=ax^2에서 x의 계수 a값이 커질 수록 경사가 가파르게 되는 것을 볼 수 있습니다.
그리고 a의 부호가 반대가 되면 x축을 기준으로 거울과 같은 모양을 가지게 됩니다.
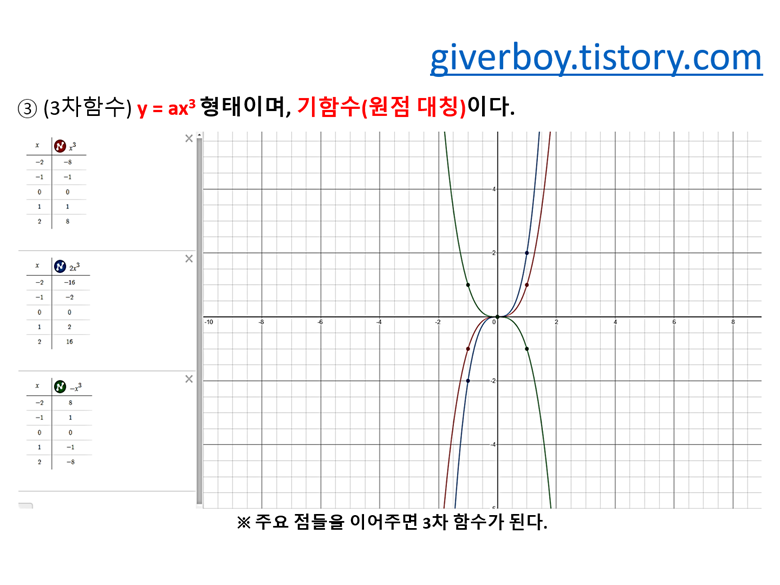
③ 3차 함수의 각 좌표를 이으면, 결국 이 함수도 선으로 표현되겠죠?^^
그 모양은 ~과 같은 모양을 가지게 됩니다.
여기에서 기함수라는 개념이 나옵니다.
기함수란, 어떤 함수가 원점 대칭인 함수를 말해요.
f(-x)=-f(x)라고 표현합니다. 이 말은 입력 -x값에 대하여 출력 y가 나오는데, 입력 x값은 -y값이 나옵니다.
입력과 출력이 서로 반대 부호를 가지고 있죠.
그래서 원점 대칭인 겁니다.
y=ax^3에서 x의 계수 값이 커질 수록 경사가 가파르다는 것을 알 수 있습니다.
모양은 y=ax의 형태와 비슷하나, 약간 곡선이 나타나네요.
그리고 부호가 반대가 되면 y축을 기준으로 거울과 같은 모양을 가지게 됩니다.
2차, 3차 함수는 문제 해석에 큰 도움이 될 수 있어요.
눈치 빠르신 분이면 알겠지만, x의 차수가 1,3,5,...홀수로 가게 되면 기함수라는 것을 우리는 알 수 있습니다.
그러나 x의 차수가 2,4,6,...짝수로 가게 되면 우함수라는 것도 유추할 수 있죠.
우함수, 기함수는 삼각함수 y=sinx, y=cosx에서도 한번 더 다룰 거예요.
너무 부담가시지 않으셨으면 합니다.
'y축 대칭이 우함수고, 원점 대칭이 기함수'라는 정도만 아세요.
항상 여러분의 꿈을 응원합니다.
부족한 글 읽어주셔서 감사합니다.
'전기기초수학' 카테고리의 다른 글
| [전기수학기초-24강]호도법의 이해 (3) | 2021.01.04 |
|---|---|
| [전기수학기초-23강]삼각비의 이해 (0) | 2020.12.29 |
| [전기수학기초-21강]함수의 기초 및 1차 함수 (1) | 2020.12.03 |
| [전기수학기초-20강]좌표의 이해 (1) | 2020.11.22 |
| [전기수학기초-19강]피타고라스의 정리 (3) | 2020.11.10 |