안녕하세요, 기버보이 입니다.
오늘은 다소 어려울 수 있는 개념인 '미적분'에 대해서 알아보도록 하겠습니다.
미적분은 미분과 적분을 이야기 하는 개념인데요.
전기기사를 공부하다 보면 가장 부담을 느끼는 챕터인데요.
사실, 고등학교 수학처럼 깊게 공부한다면 매우 어려운 단원이겠지만,
개념정도 알고, 계산하는 방법만 안다면 문제 풀이를 어려움 없이 가능할 것이라고 생각합니다.
(대학교에 배웠던 공업수학에서는 정말 극악의 난이도 였어요.)
미분 및 적분의 계산과 관련해서 저는 사용하지 안했지만, 공학용 계산기를 사용하는 방법도 있다고 하니,
공부를 해서 나중에 별도로 다루도록 하겠습니다.

① 미분과 적분은 서로 반대되는 개념입니다.
미분은 전체를 부분으로 나누는 과정이라고 생각하면 되요.
왼쪽 그럼처럼 큰 사각형을 오른쪽 그림처럼 분해가 됩니다.
사실 미분에는 시간의 개념이 많이 통용되는 되요.
우리는 어떤 전체의 과정을 부분으로 나누는 과정이라고 생각하도록 합니다.
적분은 미분의 반대 과정이라고 생각하면 되요.
나눠진 부분을 전체로 만드는 과정이예요.
역시, 어렵게 생각하지 말고, 나눠진 부분을 전체로 만드는 과정이라고만 생각 합시다.

② 미적분은 차원의 변화라고 부르도록 할께요.
사실 우리는 일상생활에서 이 부분을 알고는 있지만, 미적분의 개념이라고 인지하지 못합니다.
점은 0차원이라고 합니다. 이것들이 모이면 1차원인 선이 되고요. 1차원이 선이 모이면 2차원인 넓이가 됩니다.
그리고 2차원 면이 모이면 3차원 입체가 되게 됩니다. 3차원이 입체가 모이면 4차원이 되는 거고요.
4차원이 모이면 5차원이 되고...6차원...7차원...이렇게 늘어납니다. 수학적으로 그렇다는 거죠.
이러한 과정을 우리는 적분의 변화과정이라고 부릅니다.
역순으로 생각하게 되면 큰 부분이 작아지는 미분의 변화과정이 되는 겁니다.
아래 그림에서 첫 번째 그래프는 각 구간마다 기울기가 변화하는 즉 미분계수가 커지는 함수의 그래프를
나타낸 겁니다. 그래프가 1차함수처럼 일정하다면 미분계수는 일정한 상수가 되겠지만요.
그림과 같이 2차함수 그래프에서 각 구간마다 출력값의 기울기가 다르기 때문에 우리는 변화가 있는 함수는
부분적으로 분리하여 해석하여야 합니다.
두 번째 그래프는 그래프에서 적분이라는 것이 나왔다면, 그 함수선 아래의 넓이를 나타낸다는 것을
보여주고 싶었습니다. 삼각형이나 사각형의 넓이를 구하는 것은 매우 쉽지만, 그림처럼 함수의 그래프
면적을 구하기 위해서는 적분으로 구해야 된다는 거예요.

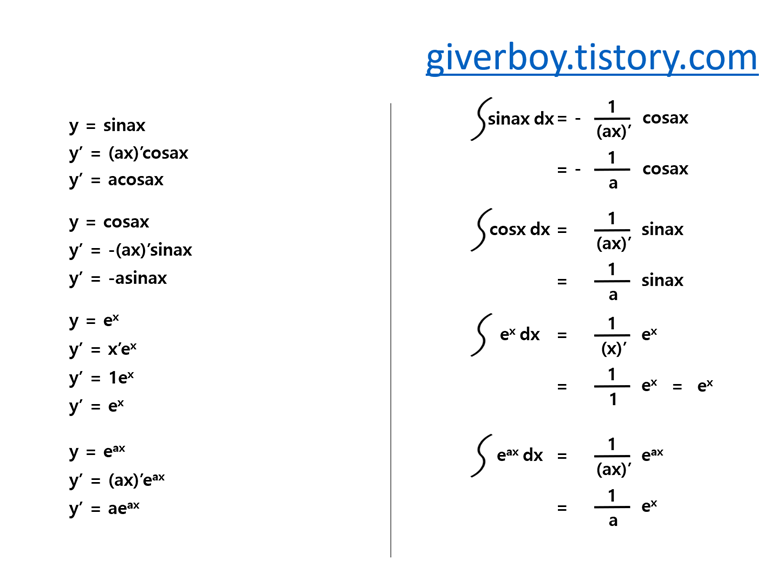
③ 위의 자료는 미적분의 기호에 대한 설명을 간단히 적어놓았어요. 더불어 전기기사에서 많이 다루는 미적분 공식들을
기재해 놓았습니다.
우선 미분부터 살펴보도록 하겠습니다.
미분은 문자 위에 '(어퍼스트로피?맞나요?)를 써서 나타냅니다. 미소한 x의 변화에 미소한 y의 변화를 보겠다는 의미죠.
이를 명확히 하기 위해, 우리는 lim이라는 극한을 사용하는데요.
어렵게 생각하시지 마시고, 'x의 변화를 0이 될 정도로 작게 보내겠습니다.' 라고 생각하시면 되요.
그리고 아래에 유용한 미분공식들을 적어놓았는데요.
외우시면 좋겠지만, 저도 자주 기억이 안나는 녀석들 입니다. 출제문제들에서 익숙해지시길 권장합니다.
적분은요. 앞에 s가 sum(합)의 s를 본따서 만든 거고요. 이것을 우리는 인테그랄이라고 부릅니다.
적분은 크게 정적분과 부정적분으로 나누어 지는데요. 정적분은 말 그대로 정해진 정분, 범위가 정해진 적분이고요.
부정적분은 범위가 정해지지 않은 적분입니다.
s에 숫자나 문자가 있으면 정적분, 없으면 부정적분 입니다. 같은 함수라면 부정적분이 좀 더 큰 값을 가지겠죠?
역시 다양한 적분 공식들을 적어놨습니다. 사실, 정적분을 이용하는 문제가 매우 많이 출제 되지 않아요.
하지만, 전자기학의 다양한 공식들을 해석함에 있어 적분이 많이 사용됩니다. 미분도 마찬가지고요.
미적분에 대한 기호의 해석이 가능하면 공식을 좀 더 유연하게 익힐 수 있게 됩니다.
저번 포스팅 때, 앞으로는 글을 자주 쓰겠다고 했는데, 시간이 지날수록 약속을 지키지 못한 점 죄송하게 생각합니다.
전기수학기초는 이번 단원을 마지막으로 공식적으로 마치려고 합니다.
필요한 부분은 지속적으로 업데이트 하겠습니다.
앞으로는 전기기사 기출문제 풀이를 할 거예요.
추후에 전자책으로 기출문제 풀이를 제공하기 때문에, 정리 전 초기풀이라도 자료가 필요하신 분은 giverboy@naver.com으로 문의 주시면 확인 후 열람 권한 드리도록 하겠습니다.
감사합니다.
'전기기초수학' 카테고리의 다른 글
| [전기수학기초-28강]행렬의 심화 (0) | 2021.03.17 |
|---|---|
| [전기수학기초-27강]행렬의 이해 (1) | 2021.02.25 |
| [전기수학기초-26강]삼각함수 그래프 해석 (1) | 2021.02.02 |
| [전기수학기초-25강]삼각함수의 의미 (1) | 2021.01.14 |
| [전기수학기초-24강]호도법의 이해 (3) | 2021.01.04 |